A Simple Note for Gaussian Mixture Models

1. Gaussian Mixture Model

A Gaussian mixture is a probabilistic model that assumes all the data points are generated from a mixture of a finite number of Gaussian distributions with unknown parameters.

scikit-learn.org

Gaussian mixture model(GMM) is an clustering algorithm similar to k-means. Unlike k-means, GMM is a soft clustering, each instance associates with a cluster with a probability. Formally, given a set of observations \(X = (x_1, x_2, ..., x_n)\), \(x_i \in R^{d}\), and \(i=1, 2, ..., n\), Gaussian mixture model assumes:

there are \(K\) mixture components, component value denoted as \(k \in \{1, 2, ..., K\}\)
\(x_i\) comes from component \(z_i\), \(Z = (z_1, z_2, ..., z_n)\) is the latent variables
\(\begin{equation} P(z_i=k) = \pi_k \end{equation}\), s.t. \(\sum_{k=1}^K \pi_k = 1\), \(\pi = (\pi_1, \pi_2, ...\pi_K)\) is the mixing proportions
\(\begin{equation} P(x_i=x | z_i=k) \sim N(\mu_k, \Sigma_k) \end{equation}\), \(N(\mu_k, \Sigma_k)\) is a multivariate Gaussian distribution, the density function is

\[\begin{equation} f(x_i) = \frac{1}{\sqrt{(2 \pi)^d \det \Sigma_k}} \exp\left( -\frac{1}{2} (x_i - \mu_k)^T \Sigma_k^{-1} (x_i - \mu_k) \right), \end{equation}\]

where \(\Sigma_k\) is the \(d \times d\) covariance matrix for component \(k\). The objective of GMM is to estimate the probabilities that each instance belongs to each component, that is

\[\begin{equation} P(z_i=k | x_i), k = 1, 2, ... K, i=1, 2, ... n \label{obj} \end{equation}\]

2. Bayes and Maximum Likelihood Estimation

With Bayes rule, we have

\[\begin{equation} \begin{aligned} P(z_i=k|x_i) & = \frac{P(x_i|z_i)P(z_i=k)}{P(x_i)} \\ & = \frac{P(x_i|z_i)P(z_i=k)}{\sum_{k=1}^KP(x_i|z_i)P(z_i=k)} \\ & = \frac{\pi_k*N(x_i, \mu_k, \Sigma_k)}{\sum_{k=1}^K\pi_k*N(x_i, \mu_k, \Sigma_k)} \\ & = w_{ik} \end{aligned} \label{weights} \end{equation}\]

If we know parameters \(\theta = (\pi_1, \pi_2, ..., \pi_K, \mu_1, \mu_2, ..., \mu_K, \Sigma_1, \Sigma_2, ..., \Sigma_K)\), we will get the objective. Therefore, the target becomes to estimate the unknown parameter \(\theta\). To estimate \(\theta\), GMM uses maximum likelihood estimation(MLE),

\[\begin{equation} \begin{aligned} L(\theta|X, Z) & = P(X, Z|\theta) \\ & = \prod_{i=1}^n \sum_{k=1}^K P(x_i=x|z_i=k)P(z_i=k) \\ & = \prod_{i=1}^n \sum_{k=1}^K \pi_k N(\mu_k, \Sigma_k) \end{aligned} \end{equation}\]

log-likelihood becomes

\[\begin{equation} \begin{aligned} l(\theta|X, Z) & = \sum_{i=1}^n log(\,\sum_{k=1}^K \pi_k N(\mu_k, \Sigma_k))\, \end{aligned} \end{equation}\]

Normally, we can get

\[\begin{equation} \theta^{*} = \underset{\theta}{\operatorname{argmax}} l(\theta|X, Z) \end{equation}\]

by set

\[\begin{equation} \frac{\partial l}{\partial \theta} = 0 \end{equation}\]

However, it’s hard to solve \(\theta\) with closed-form expressions now. So GMM uses the Expectation—maximization algorithm(EM).

3. Expectation—Maximization Algorithm

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables.

wiki

EM iterates the expectation step(E-step) and the maximization step(M-step) until converge:

initializes \(\theta = (\pi_1, \pi_2, ..., \pi_K, \mu_1, \mu_2, ..., \mu_K, \Sigma_1, \Sigma_2, ..., \Sigma_K)\) to \(\theta_0\)
start iteration until convergence or reach the max iterate number, at step \(t\geq0\):

2.1 E-step: with \(\theta_{t}\), calculates \(\begin{equation} P(z_i=k|x_i) \end{equation}\) through equation \(\eqref{weights}\) for \(k=1, 2, ..., K\) and \(i=1, 2, ..., n\)

2.2 M-step: estimates \(\theta_{t+1}\) by Maximum Likelihood Estimation

In E-step, EM defines the expected value of the log-likelihood function of \(\theta\) as

\[\begin{equation} \mathbf{Q}(\theta|\theta_{t}) = \mathbf{E}_{Z|X, \theta^t}(logL(\theta;X,Z)) \end{equation}\]

In M-step, EM estimates next \(\theta\) as

\[\begin{equation} \theta^{t+1} = \underset{\theta}{\operatorname{argmax}} \mathbf{Q}(\theta|\theta_{t}) \quad s.t. \ \sum_{k=1}^K \pi_k = 1 \end{equation}\]

4. GMM with EM

In GMM situation, we have

\[\begin{equation} \begin{aligned} L(\theta;x_i, z_i) & = \prod_{k=1}^K I(z_i=k) P(x_i, z_i|\theta) \\ & = \prod_{k=1}^K I(z_i=k) P(x_i|z_i, \theta) P(z_i | \theta) \\ & = \prod_{k=1}^K I(z_i=k) N(x_i|\mu_k, \Sigma_k) \pi_k \end{aligned} \end{equation}\]

where \(I(z_i=k)\) is a indicator function. And

\[\begin{equation} L(\theta|X, Z) = \prod_{i=1}^n L(\theta;x_i, z_i) \end{equation}\]

In E-step, the expected value of the log-likelihood function becomes

\[\begin{equation} \begin{aligned} \mathbf{Q}(\theta|\theta_{t}) & = \mathbf{E}_{Z|X, \theta^t}(logL(\theta;X,Z)) \\ & = \mathbf{E}_{Z|X, \theta^t}\sum_{i=1}^nlog(L(\theta;x_i, z_i)) \\ & = \sum_{i=1}^n \mathbf{E}_{z_i|x_i, \theta^t} log(L(\theta;x_i, z_i)) \\ & = \sum_{i=1}^n \mathbf{E}_{z_i|x_i, \theta^t} \sum_{k=1}^K I(z_i=k) *(log\pi_k + logN(x_i|\mu_k, \Sigma_k)) \\ & = \sum_{i=1}^n \sum_{k=1}^K P(z_i=k|x_i) * (log\pi_k + logN(x_i|\mu_k, \Sigma_k)) \end{aligned} \end{equation}\]

Combine the current \(\theta_{t}\) and equation \(\eqref{weights}\), we have

\[\begin{equation} w_{ik} = P(z_i=k|x_i) \end{equation}\]

where \(w_{ik}\) is a constant. Thus

\[\begin{equation} \mathbf{Q}(\theta|\theta_{t}) = \sum_{i=1}^n \sum_{k=1}^K w_{ik} * (log\pi_k + logN(x_i|\mu_k, \Sigma_k)) \end{equation}\]

In M-step, the optimal problem becomes

\[\begin{equation} \begin{aligned} \underset{\theta}{\operatorname{max}} \quad & \mathbf{Q}(\theta|\theta_{t}) \\ \text{s.t.} \quad & \sum_{k=1}^K \pi_k = 1 \end{aligned} \end{equation}\]

which is a Lagrangian problem. Therefore,

\[\begin{equation} \begin{aligned} H(\theta, \lambda) = \mathbf{Q}(\theta|\theta_{t}) + \lambda(\sum_{k=1}^K \pi_k - 1) \end{aligned} \end{equation}\]

Take partial derivatives, we have

\[\begin{equation} \begin{aligned} \frac{\partial H}{\partial \mu_k} & = \sum_{i=1}^n w_{ik} * \frac{\partial logN(x_i|\mu_k, \Sigma_k)}{\partial \mu_k} \\ & = \sum_{i=1}^n w_{ik} \Sigma_{k}^{-1}(x_i - \mu_k) \end{aligned} \label{partialmu} \end{equation}\]

and

\[\begin{equation} \frac{\partial H}{\partial \Sigma_k} = \frac{1}{2}\{ \sum_{i=1}^n w_{ik} \Sigma_{k}^{-T} (x_i - \mu_k)(x_i-\mu_k)^{T}(\Sigma^{-T} - I) \} \label{partialSigma} \end{equation}\]

and

\[\begin{equation} \frac{\partial H}{\partial \pi_k} = \sum_{i=1}^n w_{ik} / \pi_k + \lambda \label{pi_k} \end{equation}\]

and

\[\begin{equation} \frac{\partial H}{\partial \lambda} = \sum_{k=1}^K \pi_k - 1 \label{lambda} \end{equation}\]

Set \(\eqref{partialmu}\) equal to zero, we have

\[\begin{equation} \mu_k^* = \frac{\sum_{i=1}^n w_{ik}x_i}{\sum_{i=1}^n w_{ik}} \end{equation}\]

Set \(\eqref{partialSigma}\) equal to zero, and combine with \(\mu_k^*\), we have

\[\begin{equation} \Sigma_k^* = \frac{\sum_{i=1}^n w_{ik}(x_i-\mu_k)(x_i-\mu_k)^{T} }{\sum_{i=1}^n w_{ik}} \end{equation}\]

Set \(\eqref{pi_k}\) and \(\eqref{lambda}\) equal to zero, we have

\[\begin{equation} \pi_k^* = \frac{\sum_{i=1}^n w_{ik}}{\sum_{k=1}^K \sum_{i=1}^n w_{ik}} \end{equation}\]

Therefore, we got \(\theta_{t+1} = (\mu_1^*, \mu_2^*, ... \mu_K^*, \Sigma_1^*, \Sigma_2^*, ... \Sigma_K^*, \pi_1^*, \pi_2^*, ... \pi_K^*)\).

5. A numpy python implementation

First, we need to initialize \(\theta_0\). Here, we use kmeans++, kmeans and random to initialize parameters. After initialization, we calculate the weights equation \(\eqref{weights}\), which is the E-step.

# 0. import
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

X, y = make_blobs()

# 1. EM: Initlization and E-step

def _kmeans_init(X, n_component, kmeans_method):
    n_samples = X.shape[0]
    if kmeans_method == 'kmeans++':
        kmeans = KMeans(n_clusters=n_components).fit(X)
    else:
        kmeans = KMeans(n_clusters=n_components, init='random').fit(X)
    labels = kmeans.labels_
    
    weight_matrix = None
    
    for i in range(n_component):
        sub_component = X[labels==i]
        
        pi = sub_component.shape[0]/n_samples
        mean = np.mean(sub_component, axis=0)
        cov = np.cov(sub_component.T)
        
        pdf_value = multivariate_normal.pdf(X, mean, cov)
        weight = pi*pdf_value
        
        if weight_matrix is None:
            weight_matrix = weight
        else:
            weight_matrix = np.column_stack((weight_matrix, weight))
        
    weight_sum = np.sum(weight_matrix, axis=1)[:, np.newaxis]
    weights = weight_matrix/weight_sum
    return weights

def _initialize(X, n_component, method):
    # default random
    n_samples = X.shape[0]
    if method == 'kmeans++':
        weights = _kmeans_init(X, n_component, 'kmeans++')
    elif method == 'kmeans_random':
        weights = _kmeans_init(X, n_component, 'kmeans_random')
    else:
        weights = np.random.rand(n_samples, n_components)
        w = weights.sum(axis=1)
        weight_sum = weights.sum(axis=1)[:, np.newaxis]
        weights /= weight_sum
        
    return weights

Given the value of weights equation \(\eqref{weights}\), we update the value of \(\theta\) through MLE, which is the M-step. To avoid forloop, convert the numerator of equation \(\eqref{partialSigma}\) as:

\[\begin{equation} \begin{aligned} A & = \sum_{i=1}^n w_{ik}(x_i - \mu_k)(x_i - \mu_k)^T \\ \Rightarrow \quad A_{st} &= \sum_{i=1}^n w_{ik}x_{is}x_{it} - \sum_{i=1}^nw_{ik}\mu_{ks}x_{it} - \sum_{i=1}^nw_{ik}\mu_{kt}x_{is} + \sum_{i=1}^nw_{ik}\mu_{ks}\mu_{kt} \\ \Rightarrow \quad A_{st} & = A1_{st} - A2_{st} - A3_{st} + A4_{st} \end{aligned} \end{equation}\]

for \(1 \leq s, t \leq d\), where

\[\begin{equation} \begin{aligned} A1 & = w_k*(X.T) \\ A2 & = A3.T \\ A3 & = \mu_k((w_k*(X.T)).dot(H)) \\ A4 & = (\sum_{i=1}^n w_{ik})*(\mu_k.dot(\mu_k.T)) \\ w_k & = np.array([w_k1, w_k2, ... w_kn]) \\ \mu_k & = np.array([\mu_k1, \mu_k2, ..., \mu_kd]) \\ H & = np.ones(shape=(n, d)) \end{aligned} \end{equation}\]

# 2. EM: M-step

def _update_means(X, weights):
    weight_sum = np.sum(weights, axis=0)
    means = X.T.dot(weights)/weight_sum
    return means

def _update_covs(X, n_components, weights, means):
    n, m = X.shape
    covs = None
    H = np.ones(shape=(n, m))
    
    for k in range(n_components):
        weight = weights[:, k]
        weight_sum = np.sum(weight)
        mean = means[:, k]
        weighted_X_T = weight*(X.T)
        
        a1 = (weighted_X_T).dot(X)
        a3 = mean*(weighted_X_T.dot(H))
        a2 = a3.T
        mean_reshaped = mean.reshape(-1, 1)
        a4 = weight_sum*((mean_reshaped).dot(mean_reshaped.T))
        a = a1 - a2 - a3 + a4
        
        cov = a/weight_sum
        if covs is None:
            covs = cov
        else:
            covs = np.dstack((covs, cov))
    return covs

def _update_pis(weights):
    w_each_component = np.sum(weights, axis=0)
    w_sum = np.sum(w_each_component)
    pis = w_each_component/w_sum
    return pis

def _update_weights(X, n_components, means, covs, pis):
    weighted_pdf_array = None
    for k in range(n_components):
        mean = means[:, k]
        cov = covs[:,:,k]
        pi = pis[k]
        pdf_values = multivariate_normal.pdf(X, mean, cov)
        weighted_pdf_values = pi*pdf_values
        if weighted_pdf_array is None:
            weighted_pdf_array = weighted_pdf_values
        else:
            weighted_pdf_array = np.column_stack((weighted_pdf_array, weighted_pdf_values))
    
    weighted_sum = np.sum(weighted_pdf_array, axis=1)[:, np.newaxis]
    weights = weighted_pdf_array/weighted_sum
    return weights

# 3. gmm fit
def gmm_fit(X, n_components, init_method, max_iter=100):
    weights = _initialize(X, n_components, init_method)
    iter_left = max_iter
    while iter_left > 0:
        means = _update_means(X, weights)
        covs = _update_covs(X, n_components, weights, means)
        pis = _update_pis(weights)
        weights_next = _update_weights(X, n_components, means, covs, pis)
        
        if np.allclose(weights, weights_next):
            print('converage at step', max_iter-iter_left)
            break
        else:
            weights = weights_next
            iter_left -= 1
    return means, covs, weights_next

# 4. predict labels
def gmm_predict(X, n_components, means, covs, weights):
    pdf_values = None
    for k in range(n_components):
        mean = means[:, k]
        cov = covs[:, :, k]
        pdf_value = multivariate_normal.pdf(X, mean, cov)
        if pdf_values is None:
            pdf_values = pdf_value
        else:
            pdf_values = np.column_stack((pdf_values, pdf_value))
    labels = np.argmax(pdf_values, axis=1)
    return labels

# 5. gmm
def gmm_fit_predict(X, n_components, init_method, max_iter):
    means, covs, weights = gmm_fit(X, n_components, init_method, max_iter)
    labels = gmm_predict(X, n_components, means, covs, weights)
    return labels

# 6. result and demonstration
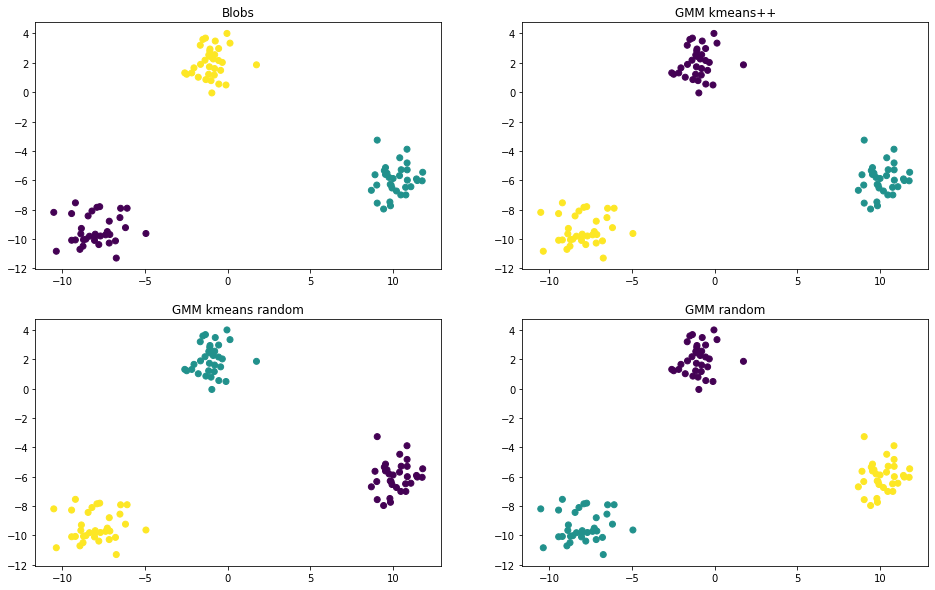
def plot_scatter(ax, X, labels, title):
    ax.scatter(X[:, 0], X[:, 1], c=labels)
    ax.set_title(title)

n_components = 3
gmm_labels_kmeans_plus_plus = gmm_fit_predict(X, n_components, 'kmeans++', max_iter=1000)
gmm_labels_kmeans_random = gmm_fit_predict(X, n_components, 'kmeans_random', max_iter=1000)
gmm_labels_random = gmm_fit_predict(X, n_components, 'random', max_iter=1000)

fig, axes = plt.subplots(2, 2, figsize=(16, 10))
plot_scatter(axes[0, 0], X, y, 'Blobs')
plot_scatter(axes[0, 1], X, gmm_labels_kmeans_plus_plus, 'kmeans++')
plot_scatter(axes[1, 0], X, gmm_labels_kmeans_random, 'kmeans random')
plot_scatter(axes[1, 1], X, gmm_labels_random, 'random')